Algoritma dalam pembuatan PiQi Plot adalah sebagai berikut :
1. Memulai perintah pemrograman.
2. Mengurutkan data bangkitan
3. Menentukan nilai Pi.
4. Menentukan nilai Qi
5. Membuat scatterplot antara nilai Qi dengan X(1).
6. Perintah pemrograman selesai.
Jumat, 02 Oktober 2009
Rabu, 16 September 2009
Minal Aidzin Wal Faidzin
MTV bilang kalo mo minta maap g ush nunggu lebaran.
Org bijak blg kerennya kalo mnt maap duluanUst.
Jefri blg org cakep mnt maap gk prl disuruh.
Kyai blg org jujur ga perlu malu utk minta maap.
Jd krn mrs anak nongkrong yg jujur, keren cakep dan baekya gw ngucapin minal aidzin wal faizin , mohon maaf lahir dan batin ..
Org bijak blg kerennya kalo mnt maap duluanUst.
Jefri blg org cakep mnt maap gk prl disuruh.
Kyai blg org jujur ga perlu malu utk minta maap.
Jd krn mrs anak nongkrong yg jujur, keren cakep dan baekya gw ngucapin minal aidzin wal faizin , mohon maaf lahir dan batin ..
Met Lebaran all
Faith makes all things possible.
Hope makes all things work.
Love makes all things beautiful.
May you have all of the three.
Happy Iedul Fitri.”
Hope makes all things work.
Love makes all things beautiful.
May you have all of the three.
Happy Iedul Fitri.”
Sabtu, 12 September 2009
Pengantar
Assalammualaikum Wr Wb
Nama : Karlinarachmasita
Nrp : 1307 100 042
Kali ini membahas mengenai pembangkitan bilangan acak pseudo-random generation. Silahkan dilihat hasil postingan saya.
Wassalam;
Nama : Karlinarachmasita
Nrp : 1307 100 042
Kali ini membahas mengenai pembangkitan bilangan acak pseudo-random generation. Silahkan dilihat hasil postingan saya.
Wassalam;
Tugas Buat function dari masing-masing distribusi
1. Uniform (a,b)
Fungsi Distribusi Uniform
Function Uniform (a,b : double) : double;
Var u : double;
Begin
u := random;
Uniform := (b-a) * u + a;
End;
2. eksponential
Function Eksponensial (beta : double) : double;
Var u : double;
Begin
u := random;
Eksponensial := -beta * ln(u);
End;
3. normal
Procedure Normal (mean,variance : double ; Var z1,z2 : double);
Var u1,u2,v1,v2,w,y,x1,x2 : double;
Begin
Repeat
u1 := random;
u2 := random;
v1 := 2 * u1 – 1;
v2 := 2 * u2 – 1;
w := sqr(v1) + sqr(v2);
if w <= 1 then
begin
y := sqrt ((-2*ln(w))/w);
x1 := v1 * y;
x2 := v2 * y;
z1 := sqrt (variance) * x1 + mean;
z2 := sqrt (variance) * x2 + mean;
end
Until w <= 1;
End;
4. lognormal
procedure lognormal (mean,varr : double;
Var zln1,zln2 : double);
Var y1, y2 : double;
begin
Normal (mean,varr,y1,y2);
zln1 := exp(y1);
zln2 := exp(y2);
end;
5. weibul
Function Weibull (alfa,beta: double) : double;
Var u,z : double;
Begin
u := random;
z := -ln(u);
Weibull := beta * exp (ln(z)/alfa);
End;
6. t-student
function tdistribution(m:integer):double;
Fungsi Distribusi Uniform
Function Uniform (a,b : double) : double;
Var u : double;
Begin
u := random;
Uniform := (b-a) * u + a;
End;
2. eksponential
Function Eksponensial (beta : double) : double;
Var u : double;
Begin
u := random;
Eksponensial := -beta * ln(u);
End;
3. normal
Procedure Normal (mean,variance : double ; Var z1,z2 : double);
Var u1,u2,v1,v2,w,y,x1,x2 : double;
Begin
Repeat
u1 := random;
u2 := random;
v1 := 2 * u1 – 1;
v2 := 2 * u2 – 1;
w := sqr(v1) + sqr(v2);
if w <= 1 then
begin
y := sqrt ((-2*ln(w))/w);
x1 := v1 * y;
x2 := v2 * y;
z1 := sqrt (variance) * x1 + mean;
z2 := sqrt (variance) * x2 + mean;
end
Until w <= 1;
End;
4. lognormal
procedure lognormal (mean,varr : double;
Var zln1,zln2 : double);
Var y1, y2 : double;
begin
Normal (mean,varr,y1,y2);
zln1 := exp(y1);
zln2 := exp(y2);
end;
5. weibul
Function Weibull (alfa,beta: double) : double;
Var u,z : double;
Begin
u := random;
z := -ln(u);
Weibull := beta * exp (ln(z)/alfa);
End;
6. t-student
function tdistribution(m:integer):double;
Label r2;
Var v,x,r,s,c,a,f,g,mm : real;
begin
mm:=0;
if m < 1 then
begin
writeln('impermissible degrees of freedom.');
halt;
end;
if (m mm) then
begin
s:=m;
c:=-0.25*(s+1);
a:=4/power((1+1/s),c);
f:=16/a;
if m>1 then
begin
g:=s-1;
g:=power(((s+1)/g),c)*sqrt((s+s)/g);
end else
g := 1;
mm:=m;
end;
r2:repeat
r:=random;
until r > 0.0;
x:=(2*random-1)*g/r;
v:=x*x;
if (v>(5-a*r)) then
begin
if ((m>=3) and (r*(v+3)>f)) then goto r2;
if (r>power((1+v/s),c)) then goto r2;
end;
tdistribution :=x;
end;
begin
tipe11[1]:=0.2;
tipe11[1]:=0.3;
tipe11[1]:=0.5;
tipe11[1]:=0.8;
tipe11[1]:=1.0;
end.
Kuliah Teknik Simulasi untuk minggu ke-3
Pembangkitan Bilangan Acak
Pseudo-Random Generation
Random yang semu
Karena barisan bilangan random dihasilkan bilangan suatu rumus :
xn = axn-1 Modulo M
Misal :
a = 2, M = 5, xo = 3
x1 = 2(3) modulo 5 = 1
x2 = 2(1) modulo 5 = 2
x3 = 2(2) modulo 5 = 4
x4 = 2(4) modulo 5 = 3
Bilangan Biner :
I = 1
II = 3
III = 7
Rumus untuk pseudo-random dapat diberikan seperti:
xn = axn-1 Modulo M
x ~ u(a,b)
function uniform (a,b:real):real;
begin
uniform:=a+(b-a)x random;
end;
invers transform
F(x)= u, u ~ u(0,1)
x =...?
u ~ u(0,1)
f(x) = 1 - e-x
F(x) = u
1 - e-x = u
e-x = 1 – u
Perintah ln di dalam Pascal
Function expo (mean:real):real;
Begin
expo = -loge(random)*mean;
end;
jika merandom data pada distribusi uniform dengan bantuan software minitab :
MTB > Random 1000 c1;
SUBC > Uniform 0,0 1,0.
MTB > Random 1000 c2;
SUBC > Uniform 0,0 1,0.
MTB > Plot c1*c2;
SUBC > symbol.
untuk lebih lengkapnya saya tampilkan dalam bentuk download mengenai distribusi uniform, eksponensial, dan normal. silahkan klik di sini :
http://rapidshare.com/files/279287706/Beberapa_Distribusi_Khusus.doc.htmlLink yang tersedia
Anda bisa lihat link yang tersedia di sini mengenai pembangkitan bilangan acak dan bilangan biner pada waktu kuliah simulasi minngu ke-3:
http://www.its.ac.id/
http://www.google.co.id/
https://www.blogger.com/start
http://www.google.co.id/#hl=id&q=function+dari+distribusi+uniform&meta=&fp=ead79af733d7a7f8
http://id.wikipedia.org/wiki/Sistem_bilangan_biner
http://www.google.co.id/#hl=id&q=bilangan+biner&meta=&fp=ead79af733d7a7f8
http://www.its.ac.id/
http://www.google.co.id/
https://www.blogger.com/start
http://www.google.co.id/#hl=id&q=function+dari+distribusi+uniform&meta=&fp=ead79af733d7a7f8
http://id.wikipedia.org/wiki/Sistem_bilangan_biner
http://www.google.co.id/#hl=id&q=bilangan+biner&meta=&fp=ead79af733d7a7f8
Beberapa Distribusi Khusus
Beberapa Distribusi Khusus
Distribusi Uniform
• Distribusi uniform sering digunakan jika tdk diketahui ‘pengetahuan awal’ dari pdf dan semua harga dlm range kelihatannya ‘equally likely’
Mean dan Variance dari Distribusi Uniform
Ilustrasi Distribusi Uniform
Distribusi Eksponensial
Properti yg paling penting adalah “memoryless”
Mean dan Variance Distribusi Eksponensial
Distribusi Eksponensial
Distribusi Normal (Gaussian)
Mean dan Variance Distribusi Normal (Gaussian)
mX = E(X) = m
sX2 = Var(X) = s2
Distribusi Normal (Gaussian)
SISTEM BILANGAN BINER
SISTEM BILANGAN BINER
Sistem bilangan biner merupakan sistem bilangan dengan basis 2. Sistem bilangan biner menggunakan dua buah simbol yaitu : 0 dan 1. Contoh bilangan biner adalah 1001 yang dapat diartikan dalam sistem bilangan desimal menjadi sebagai berikut :
Position value dalam sistem bilangan biner merupakan perpangkatan dari nilai 2.
Nilai desimal dari sistem bilangan biner juga dapat dicari menggunakan rumus dibawah ini.
Pertambahan Bilangan BINER
Pertambahan pada sistem bilangan biner dilakukan dengan cara yang sama dengan pertambahan pada sistem bilangan desimal. Dasar dari pertambahan sistem bilangan biner dapat dilihat pada gambar dibawah ini.
Pengurangan Bilangan BINER
Pengurangan pada sistem bilangan BINER dilakukan dengan cara yang sama dengan pengurangan sistem bilangan desimal. Dasar dari pengurangan sistem bilangan BINER dapat dilihat pada gambar dibawah ini.
Contoh pengurangan bilangan biner:
Pengurangan bilangan biner juga dapat dilakukan dengan menggunakan Komplemen. Terdapat dua macam komplemen pada sistem bilangan biner yaitu : Komplemen 1 (1s complement) dan Komplemen 2 (2s complement).
Contoh pengurangan bilangan biner menggunakan komplemen 1 :
Komplemen 2 adalah hasil dari komplemen 1 ditambah 1, misalnya komplemen 2 dari bilangan BINER 10110 adalah 01010 (dari komplemen 1 yaitu 01001 ditambah 1). Dengan menggunakan komplemen 2, hasil digit paling kanan dibuang, tidak digunakan.
Perkalian Bilangan BINER
Perkalian bilangan biner dilakukan dengan cara yang sama dengan perkalian pada sistem bilangan desimal.
Perhatikan, ada dua keadaan dalam perkalian bilangan biner, jika pengali adalah bilangan 1 maka cukup disalin saja, jika pengali adalah bilangan 0 maka hasilnya semuanya 0.
Pembagian Bilangan Biner
Pembagian bilangan biner juga dilakukan dengan cara yang sama dengan pembagian bilangan desimal. Pembagian dengan 0 tidak mempunyai arti, sehingga dasar untuk pembagian menjadi seperti dibawah ini.
Sistem bilangan biner
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Sistem bilangan biner atau sistem bilangan basis dua adalah sebuah sistem penulisan angka dengan menggunakan dua simbol yaitu 0 dan 1. Sistem bilangan biner modern ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Dari sistem biner, kita dapat mengkonversinya ke sistem bilangan Oktal atau Hexadesimal. Sistem ini juga dapat kita sebut dengan istilah bit, atau Binary Digit. Pengelompokan biner dalam komputer selalu berjumlah 8, dengan istilah 1 Byte. Dalam istilah komputer, 1 Byte = 8 bit. Kode-kode rancang bangun komputer, seperti ASCII, American Standard Code for Information Interchange menggunakan sistem peng-kode-an 1 Byte.
Bilangan desimal yang dinyatakan sebagai bilangan biner akan berbentuk sebagai berikut:
| Desimal | Biner (8 bit) |
| 0 | 0000 0000 |
| 1 | 0000 0001 |
| 2 | 0000 0010 |
| 3 | 0000 0011 |
| 4 | 0000 0100 |
| 5 | 0000 0101 |
| 6 | 0000 0110 |
| 7 | 0000 0111 |
| 8 | 0000 1000 |
| 9 | 0000 1001 |
| 10 | 0000 1010 |
| 11 | 0000 1011 |
| 12 | 0000 1100 |
| 13 | 0000 1101 |
| 14 | 0000 1110 |
| 15 | 0000 1111 |
| 16 | 0001 0000 |
20=1
21=2
22=4
23=8
24=16
25=32
26=64
dst
contoh: mengubah bilangan desimal menjadi biner
desimal = 10.
berdasarkan referensi diatas yang mendekati bilangan 10 adalah 8 (23), selanjutnya hasil pengurangan 10-8 = 2 (21). sehingga dapat dijabarkan seperti berikut
10 = (1 x 23) + (0 x 22) + (1 x 21) + (0 x 20).
dari perhitungan di atas bilangan biner dari 10 adalah 1010
dapat juga dengan cara lain yaitu 10 : 2 = 5 sisa 0 (0 akan menjadi angka terakhir dalam bilangan biner), 5(hasil pembagian pertama) : 2 = 2 sisa 1 (1 akan menjadi angka kedua terakhir dalam bilangan biner), 2(hasil pembagian kedua): 2 = 1 sisa 0(0 akan menjadi angka ketiga terakhir dalam bilangan biner), 1 (hasil pembagian ketiga): 2 = 0 sisa 1 (0 akan menjadi angka pertama dalam bilangan biner) karena hasil bagi sudah 0 atau habis, sehingga bilangan biner dari 10 = 1010
atau dengan cara yang singkat 10:2=5(0),5:2=2(1),2:2=1(0),1:2=0(1)sisa hasil bagi dibaca dari belakang menjadi 1010
Blum Blum Shut (BBS)
- CSPRNG yang paling sederhana dan paling mangkus (secara kompleksitas teoritis).
- BBS dibuat pada tahun 1986 oleh Lenore Blum, Manuel Blum, dan Michael Shub.
- Berbasis teori bilangan
Algoritma:
- Pilih dua buah bilangan prima rahasia, p dan q, yang masing-masing kongruen dengan 3 modulo 4.
- Kalikan keduanya menjadi n = pq. Bilangan m ini disebut bilangan bulat Blum
- Pilih bilangan bulat acak lain, s, sebagai umpan sedemikian sehingga:
(i) 2 £ s < n
(ii) s dan n relatif prima
kemudian hitung x0 = s2 mod n
- Barisan bit acak dihasilkan dengan melakukan iterasi berikut sepanjang yang diinginkan:
- (i) Hitung xi = xi – 1 2 mod n
- (ii) zi = bit LSB (Least Significant Bit) dari xi
Barisan bit acak adalah z1, z2, z3, …
- Bilangan acak tidak harus 1 bit LSB tetapi bisa juga j buah bit (j adalah bilangan bulat positif yang tidak melebihi log2(log2 n)) ).
- Perhatikan contoh berikut:
- Keamanan BBS terletak pada sulitnya memfaktorkan n. Nilai n tidak perlu rahasia dan dapat diumumkan kepada publik.
- BBS tidak dapat diprediksi dari arah kiri (unpredictable to the left) dan tidak dapat diprediksi dari arah kanan (unpredictable to the kanan),
- artinya jika diberikan barisan bit yang dihasilkan oleh BBS, kriptanalis tidak dapat memprediksi barisan bit sebelumnya dan barsian nit sesudahnya
CSPRNG Berbasis RSA
- Pilih dua buah bilangan prima rahasia, p dan q, dan bilangan bulat e yang relatif prima dengan (p – 1)(q – 1)
- Kalikan keduanya menjadi n = pq
- Pilih bilangan bulat acak lain, s, sebagai x0 yang dalam hal ini 2 £ s £ n
- Barisan bit acak dihasilkan dengan melakukan iterasi berikut sepanjang yang diinginkan:
a. Hitung xi = xi – 1 e mod n degan x0 = s.
b. zi = bit LSB (Least Significant Bit) dari xi
5. Barisan bit acak adalah z1, z2, z3, …
Jenis PRNG yang dibahas disini adalah Linear Congruential Generator (LCG)
Jenis PRNG yang dibahas disini adalah Linear Congruential Generator (LCG) . LCG merupakan jenis PRNGs yang banyak digunakan dalam aplikasi komputer modern. LCG ditemukan oleh D.H Lehmer. Tak lama sesudah itu, banyak programmer yang menggunakan metode LCG tersebut untuk menghasilkan bilangan yang tampak random (pseudorandom number) dalam jumlah besar dan waktu yang cepat. Programmer pada saat itu hanya membutuhkan kecepatan pembangkitan bilangan random saja, tanpa memperhatikan kerandoman bilangan tersebut secara statistika. Karena itu, ada banyak generator LCG yang gagal melalui pengujian kerandoman statistika. Linear Congruent Method banyak dipakai untuk mengbangkitkan bilangan acak Y1, Y2, Y3…, Yn yang bernilai [0,m] dengan memanfaatkan nilai sebelumnya. Untuk membangkitkan bilangan acak ke-n+1 (Yn+1) dengan LCM, didapat definisi: I(n+1) =(aI(n)+c) mod m
Keterangan:
I(n+1) = bilangan random baru yang dihasilkan
In = nilai awal atau nilai sebelumnya
a = parameter
c = parameter
m = parameter dengan a, c dan m sebagai nilai pembangkit dan I0 sebagai nilai awal
Di dalam buku teks statistik klasik, angka-angka acak diciptakan dengan mengambil bola yang dinomori ke luar dari suatu kotak yang berisi sejumlah bola bernomor yang diketahui jumlahnya. Jika jumlah bola yang ada didalam kotak jumlahnya sedikit, maka hal tersebut masih mungkin dilakukan. Tetapi jika jumlah bolanya dalam jumlah yang sangat besar, maka hal tersebut akan susah dan tidak efektif dilakukan. Terlepas dari hal itu, ada isu yang lain yang meragukan bahwa mengambil bola bernomor dari suatu kotak besar merupakan suatu proses acak dengan kesempatan sama untuk semua bola. Karena hal tersebut dan pertimbangan lainnya, maka dilakukan komputerisasi generator bilangan random/acak. Sesungguhnya, bahasa pemrograman tingkat tinggi menawarkan sedikitnya satu format dari generator bilangan random. Pembuatan angkaangka yang acak bukan merupakan hal yang mudah, karena komputer adalah suatu mesin deterministik. Karena itulah mustahil untuk membuat angka-angka acak/bilangan yang benar-benar random tanpa adanya perangkat keras tambahan.
True random number secara definisi tidak dapat terprediksi. TRNG dilakukan dengan melakukan sampling entropi sumber dari alam dan memprosesnya melalui komputer. Misalnya adalah bilangan random yang dihasilkan oleh Random.org dan Laverand.sgi.com. Random.org menggunakan atmospheric noise dari radio dan Lavarand.sgi.com menggunakan Lava Lite® lamps sebagai entropi sumber. Entropi sumber yang lain yang cukup bagus adalah radioaktivitas yang juga digunakan oleh Fourmilab di Swiss untuk membangkitkan true random number. Pseudorandom Number Generator (PNRG) atau dalam bahasa
Pembangkitan Bilangan Acak PSEUDO-RANDOM GENERATION
Pembangkit Bilangan Acak Semu
- Bilangan acak: bilangan yang tidak dapat diprediksi
- Bilangan acak (random) banyak digunakan di dalam kriptografi
- Misalnya untuk pembangkitan parameter kunci pada algoritma kunci-publik, pembangkitan initialization vector (IV) pada algoritma kunci-simetri, dan sebagainya.
- Tidak ada komputasi yang benar-benar menghasilkan deret bilangan acak secara sempurna.
- Bilangan acak yang dihasilkan dengan rumus-rumus matematika adalah bilangan acak semu (pseudo), karena pembangkitan bilangannya dapat diulang kembali.
- Pembangkit deret bilangan acak semacam itu disebut pseudo-random number generator (PRNG)
Linear Congruential Generator (LCG)
- Pembangkit bilangan acak kongruen-lanjar (linear congruential generator atau LCG ) adalah PRNG yang berbentuk:
Xn = (aXn – 1 + b) mod m
Xn = bilangan acak ke-n dari deretnya
Xn – 1 = bilangan acak sebelumnya
a = faktor pengali
b = increment
m = modulus
Kunci pembangkit adalah X0 yang disebut umpan (seed).
- LCG mempunyai periode tidak lebih besar dari m, dan pada kebanyakan kasus periodenya kurang dari itu.
- LCG mempunyai periode penuh (m – 1) jika memenuhi syarat berikut:
- b relatif prima terhadap m.
- a – 1 dapat dibagi dengan semua faktor prima dari m
- a – 1 adalah kelipatan 4 jika m adalah kelipatan 4
- m > maks(a, b, x0)
- a > 0, b > 0
- Keunggulan LCG terletak pada kecepatannya dan hanya membutuhkan sedikit operasi bit.
- Sayangnya, LCG tidak dapat digunakan untuk kriptografi karena bilangan acaknya dapat diprediksi urutan kemunculannya.
- Oleh karena itu LCG tidak aman digunakan untuk kriptografi. Namun demikian, LCG tetap berguna untuk aplikasi non-kriptografi seperti simulasi, sebab LCG mangkus dan memperlihatkan sifat statistik yang bagus dan sangat tepat untuk uji-uji empirik
Pembangkit Bilangan Acak yang Aman untuk Kriptografi
- Pembangkit bilangan acak yang cocok untuk kriptografi dinamakan cryptographically secure pseudorandom generator (CSPRNG).
- Persyaratan CSPRNG adalah:
- Secara statistik ia mempunyai sifat-sifat yang bagus (yaitu lolos uji keacakan statistik).
- Tahan terhadap serangan (attack) yang serius. Serangan ini bertujuan untuk memprediksi bilangan acak yang dihasilkan.
Jumat, 11 September 2009
Sabtu, 05 September 2009
Teknik Simulasi untuk pertemuan ke-2
Assalammualaikum Wr Wb
Nama : Karlinarachmasita
Nrp : 1307 100 042
Kali ini membahas mengenai contoh simulasi sederhana yaitu mencari pendekatan nilai pi, dan mencari pendekatan nilai variansi. Silahkan dilihat hasil postingan saya.
Wassalam;
Nama : Karlinarachmasita
Nrp : 1307 100 042
Kali ini membahas mengenai contoh simulasi sederhana yaitu mencari pendekatan nilai pi, dan mencari pendekatan nilai variansi. Silahkan dilihat hasil postingan saya.
Wassalam;
Link yang tersedia
Mengenai simulasi??Silakan liat _@@_
http://www.its.ac.id/
http://www.google.co.id/
https://www.blogger.com/start
http://zawa.blogsome.com/?s=indonesia+2009&paged=2
http://ibnuhajar.blog.friendster.com/materi-kuliah/
http://rovicky.wordpress.com/2008/02/24/simulasi-komputer-gempa-dan-tsunami-di-padang/
http://te.ugm.ac.id/~risanuri/v01/?p=66
http://sutanto.staff.uns.ac.id/2008/09/20/budaya-antri-dan-teori-antrian/
http://www.itpin.com/blog/index.php?s=komponen&paged=4
http://www.telkomrdc-media.com/index.php?ch=8&lang=s=f79d6458b43ea08dcf8348425307cbec&n=265&page=5s=f79d6458b43ea08dcf8348425307cbec&n=265&page=5
http://www.its.ac.id/
http://www.google.co.id/
https://www.blogger.com/start
http://zawa.blogsome.com/?s=indonesia+2009&paged=2
http://ibnuhajar.blog.friendster.com/materi-kuliah/
http://rovicky.wordpress.com/2008/02/24/simulasi-komputer-gempa-dan-tsunami-di-padang/
http://te.ugm.ac.id/~risanuri/v01/?p=66
http://sutanto.staff.uns.ac.id/2008/09/20/budaya-antri-dan-teori-antrian/
http://www.itpin.com/blog/index.php?s=komponen&paged=4
http://www.telkomrdc-media.com/index.php?ch=8&lang=s=f79d6458b43ea08dcf8348425307cbec&n=265&page=5s=f79d6458b43ea08dcf8348425307cbec&n=265&page=5
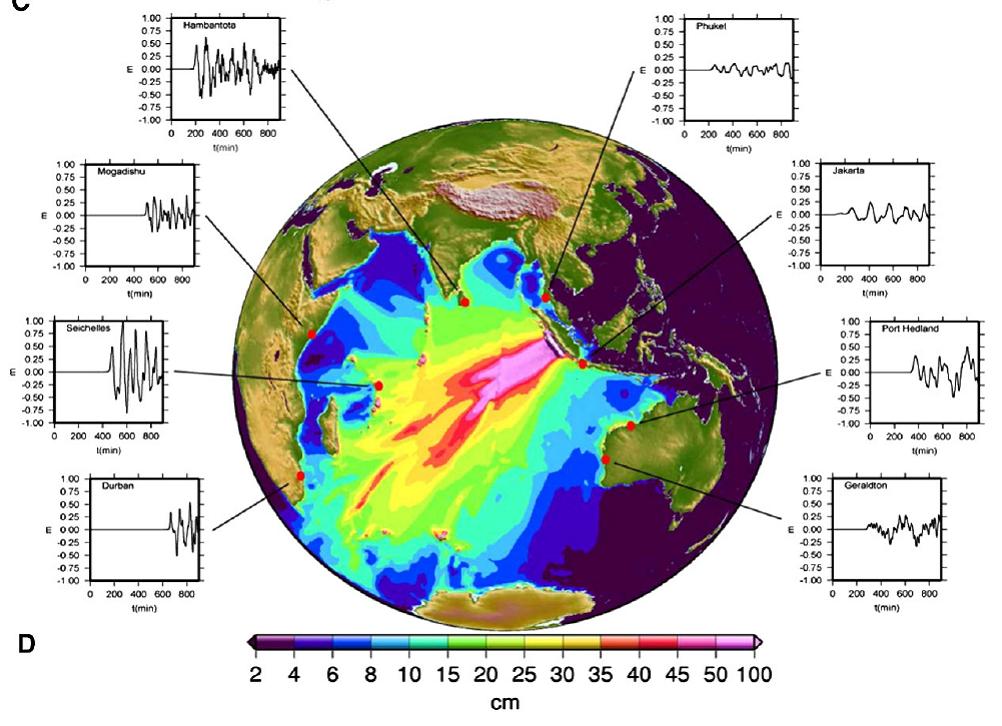
Model Tsunami Hasil Simulasi Komputer
Dibawah ini model tsunami hasil simulasi komputer itu. Dibawah ini perkiraan terbnaik yang dapat dilakukan dengan data, asumsi, serta metode yang ada. Tentusaja kalau ada perbedaan data, perbedaan asumsi, mapun metode, akan menghasilkan model simulasi komputer yang berbeda. Tentusaja model tsunami ini harus selalu diperbaharui sesuai dengan perubahan-perubahan dari data serta perkembangan ilmu pengetahuan.
Jadi dapat dipelajari bahwa seandainya terjadi tsunami di Padang dan Bengkulu, maka kemungkinan besarnya Magnitude gempa akan >M8. Skali lagi bisa juga yang terjadi gempa kecil-kecil, seperti di Bengkulu waktu itu. Dan besarnya tinggi gelombang tsunami akan kurang dari5m. Walaupun tinggi gelombang tsunami diatas 5m bisa saja terjadi dibeberapa tempat. Dengan demikian kalau saja ini membuat tembok penghalang tsunami perlu memperkirakan ketahanan terhadap getaran gempa serta gempuran gelombang tsunami ini.
Contoh Simulasi Sederhana itu seperti apa c??
Simulasi Komputer : Gempa dan Tsunami di Padang
Kejadian gempa di Simeulue pekan lalu mengingatkan aku akan sebuah artikel yang aku baca beberapa waktu lalu di Earth and Planetary Science Letters awal tahun 2008 ini. Artikel ilmiah berjudul “Tsunami threat in the Indian Ocean from a future megathrust earthquake west of Sumatra“ ini berisi hasil simulasi dengan program komputer seandainya terjadi gempa besar di laut sebelah barat Padang. Tentunya ini bukan untuk menakut-nakuti atau membuat panik. Tetapi ini merupakan kajian ilmiah apabila sesuatu terjadi. Perlu diketahui ini juga bukan ramalan atau amaran (warning).
Kejadian gempa di Simeulue pekan lalu mengingatkan aku akan sebuah artikel yang aku baca beberapa waktu lalu di Earth and Planetary Science Letters awal tahun 2008 ini. Artikel ilmiah berjudul “Tsunami threat in the Indian Ocean from a future megathrust earthquake west of Sumatra“ ini berisi hasil simulasi dengan program komputer seandainya terjadi gempa besar di laut sebelah barat Padang. Tentunya ini bukan untuk menakut-nakuti atau membuat panik. Tetapi ini merupakan kajian ilmiah apabila sesuatu terjadi. Perlu diketahui ini juga bukan ramalan atau amaran (warning).
Lokasi yang diperkirakan atau disimulasikan.
Mengingat kejadian gempa-gempa besar sebelumnya, maka dipilihlah lokasi disebelah barat kota Padang ini karena kejadian gempa dan tsunami Aceh tahun 2004, kemudian gempa Nias dan selanjutnya ke selatan seperti yang terlihat pada gambar disamping ini.
Pemilihan atau penentuan lokasi dimana yang mungkin akan terjadi ini tentu saja juga merupakan bagian dari studi mitigasi pra-bencana. Hasilnya tentu saja merupakan sebuah informasi penting dalam persiapan menghadapi apabila nantinya benar-benar terjadi.
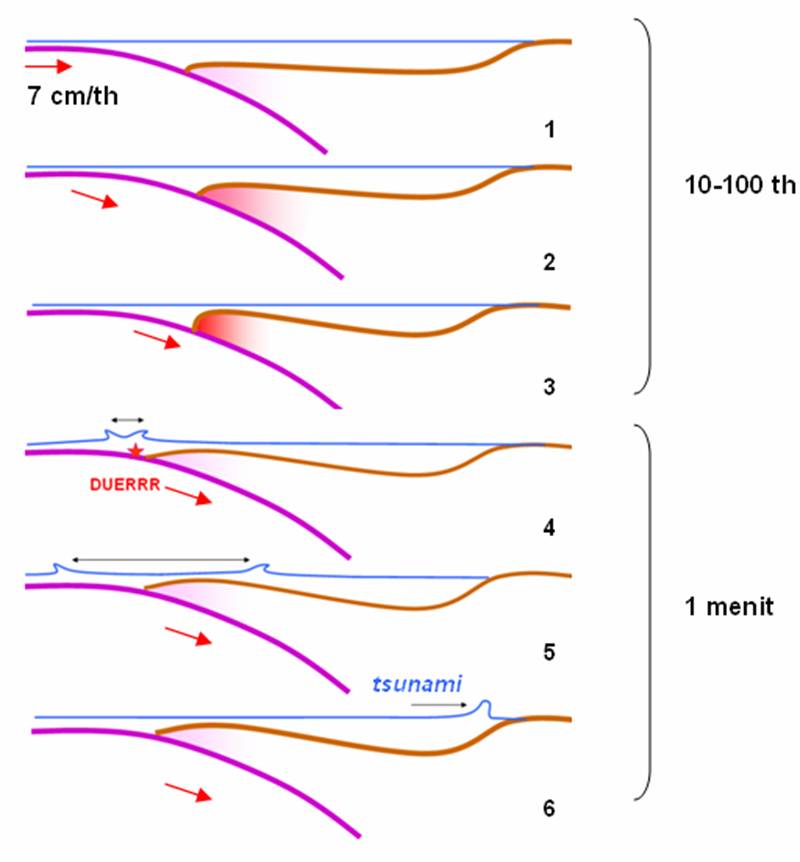
Dari gempa-gempa yang barusaja terjadi pada 5 tahun terakhir menunjukkan dua segment utama Aceh dan Nias yang sudah bergeser dan robek. Sedangkan yang disebelah selatannya justru merupakan tempat-tempat dimana ada tekanan dan energi yang masih terkumpul yang belum terlepaskan. Kalau saja akan terjadi tentusaja yang disebelah selatannya lebih mungkin terjadi ketimbang yang barusaja bergerak itu. Sedangkan robeknya disebelah utara mungkin kecil karena energi (stress) yang terkumpul di segmen itu sudah jauuh berkurang.
Mekanisme terjadinya tsunami masih ingat kaan ? OK deh kalau lupa dilihat diklik gambar diatas itu. Setelah tenaga terkumpul diujung tabrakan lempeng, maka ketika tenaga terlepaskan terjadi gempa dan gerakan ke atas ini mempengaruhi tubuh air diatasnya. Gelombang yang timbul akan bergerak dikedua arah kiri dan kanan. Waktu tempuh gelombang tsunami ini dari saat terjadinya gempa hingga mencapai pantai barat sumatra hanya dalam waktu kira-kira 20-40 menit saja, tergantung kedalaman air.
Perkiraan besarnya kekuatan gempa akan memiliki besaran >8M. Besaran angka ini diperoleh berdasarkan asumsi tenaga yang terkumpul hingga saat ini dari survey geodinamika tektonik didaerah ini. Kekuatan gempa yang >M8 ini akan mungkin menyebabkan rupture atau sobekan sepanjang 630 Kilometer !. Apakah pasti akan >8 ? Wah ini pertanyaan sukar dijawab tentusaja. Yang menjadikan susah dijawab adalah kata “pasti“. Science tidak akan menjawab sesuatu yang akan datang sebagai sebuah kepastian, tetapi pendekatan dengan probabilitas itu bisa saja. Kemungkinan akan terjadi gempa >8M memiliki kemungkinan yang cukup tinggi (misal diatas 50%).
Simulasi komputer.
Secara sederhana cara kerja simulasi ini dapat digambarkan seperti dibawah ini.
Tentusaja ada parameter dasar yang dipakai sebagai dasar pembuatan simulasi ini, antara lain data kegempaan sebelumnya, topografi dasar laut (bathimetri), topografi pantai dsb. Juga yang tidak kalah penting adalah harus ada asumsi-asumsi yang akan dipakai. Asumsi ini diperlukan karena kita tidak tahu apa yang akan terjadi. Namun asumsi-asumsi ini tentusaja tidak dapat lepas dari kenyataan historis yang pernah ada. Tidak akan mungkin menggunakan asumsi ngawur, tidak akan trus dengan asumsi rupture atau robekan dengan pergeseran vertikal 100 meter, karena asumsi ini tidak didukung dengan pengalaman. Jadi asumsi juga tidak boleh sembarangan.
Mencari pendekatan nilai variansi
Data sample yang diambil secara random ditetapkan berdistribusi normal dengan rata-rata 60 dan varians 1. Sebelum dibuat programnya kita harus membuat algoritmanya terlebih dahulu. Berikut algoritmanya di bawah ini :
1. Mulai
2. Dibangkitkan data x berdistribusi normal dengan rata-rata 60 dan varians 1 sebanyak 100 sebagai populasi
3. Diambil sample sebanyak 10 buah kemudian dihitung dan nilai variansnya
4. Diulangi langkah no 3 sebanyak 1000 kali
5. Dihitung bias dari S12 dan S22
6. Dibandingkan hasil dari langkah no 5
7. Selesai
penyelesaian :
menggunakan program Minitab yaitu sebagai berikut:
http://dzulcyber.blogspot.com/2008/08/download-pascal-tutorial.html
http://ibnuhajar.blog.friendster.com/materi-kuliah/
1. Mulai
2. Dibangkitkan data x berdistribusi normal dengan rata-rata 60 dan varians 1 sebanyak 100 sebagai populasi
3. Diambil sample sebanyak 10 buah kemudian dihitung dan nilai variansnya
4. Diulangi langkah no 3 sebanyak 1000 kali
5. Dihitung bias dari S12 dan S22
6. Dibandingkan hasil dari langkah no 5
7. Selesai
penyelesaian :
menggunakan program Minitab yaitu sebagai berikut:macro
bootvar x
mconstant i n b lower upper stat_b se_b
mcolumn x y stat
let n=10
let b=1000
do i=1:b
sample n x y;
replacement.
let stat(i)=stde(y)**2
enddo
let stat_b=mean(stat)
let se_b=stde(stat)
histo stat
sort stat stat
let lower=stat(25)
let upper=stat(975)
print stat_b se_b lower upper
endmacro
kesimpulan : nilai standart deviasi tersebut masih bias terhadap nilai parameter yang diduga.
http://dzulcyber.blogspot.com/2008/08/download-pascal-tutorial.html
http://ibnuhajar.blog.friendster.com/materi-kuliah/
Mencari Pendekatan Nilai Phi
Bahasa pemrograman (programming language)
Komputer mengerjakan transformasi data berdasarkan kumpulan perintah – program – yang telah dibuat oleh pemrogram. Kumpulan perintah ini harus dimengerti oleh komputer, berstruktur tertentu (syntax) dan bermakna. Bahasa pemrograman merupakan notasi untuk memberikan secara tepat program komputer. Berbeda dengan bahasa alamiah, mis. Bahasa Indonesia, Inggris dsb. yang merupakan bahasa alamiah(natural language), sintaks dan semantik bahasa pemrograman (komputer) ditentukan secara kaku, sehingga bahasa pemrograman juga disebut sebagai bahasa formal (formal language).
Jadi, dalam bahasa pemrograman yang digunakan sebagai alat komunikasi untuk memberikan perintah kepada komputer tidak berlaku kebebasan berekspresi seperti laiknya dalam bahasa alamiah.
Pemrograman dalam pengertian luas meliputi seluruh kegiatan yang tercakup dalam pembuatan program, termasuk analisis kebutuhan (requirement’s analysis) dan keseluruhan tahapan dalam perencanaan (planning) , perancangan (design) dan pewujudannya (implementation).
Simulasi dibuat dengan menggunakan program Pascal, dengan terlebih dahulu harus dibuat suatu algoritmanya. Berikut algoritma program untuk menghitung nilai phi1 sebagai berikut:
1. Mulai
2. Ditetapkan i:=0
3. i:=i+1
4. Dibangkitkan 10000 titik
x ~ U(0,1) dan y ~ U(0,1)
5. Ditetapkan nilai phi:=4*m/n
6. Jika i < 1000 kembali ke langkah 3
7. Nilai phi sama dengan jumlahan dari tiap phi dibagi 1000
8. Ditulis nilai phi
9. Selesai
program phi1;
uses wincrt;
var x,y,p:real;
i,m,n:integer;
begin
randomize;
n:=10000;
m:=0;
for i:=1 to n do
begin
x:=random;
y:=random;
if(x*x+y*y)<=1 then m:=m+1; end; p:=4*m/n; writeln(p); end.
Selanjutnya akan dibuat program kedua dengan menambah variabel s yaitu sebagai banyaknya sampel yang diambil diulang sampai 1000 kali sebagai berikut : program phi2; uses wincrt; var x,y,p,s:real; j,i,m,n:integer; begin s:=0; begin randomize; n:=10000; m:=0; for i:=1 to n do begin x:=random; y:=random; if(x*x+y*y)<=1 then m:=m+1; end; p:=4*m/n; s:=s+p; end; p:=s/1000; writeln(p); end.
bila diterapkan pada program dhelpi adalah sebagai berikut:
Komputer mengerjakan transformasi data berdasarkan kumpulan perintah – program – yang telah dibuat oleh pemrogram. Kumpulan perintah ini harus dimengerti oleh komputer, berstruktur tertentu (syntax) dan bermakna. Bahasa pemrograman merupakan notasi untuk memberikan secara tepat program komputer. Berbeda dengan bahasa alamiah, mis. Bahasa Indonesia, Inggris dsb. yang merupakan bahasa alamiah(natural language), sintaks dan semantik bahasa pemrograman (komputer) ditentukan secara kaku, sehingga bahasa pemrograman juga disebut sebagai bahasa formal (formal language).
Jadi, dalam bahasa pemrograman yang digunakan sebagai alat komunikasi untuk memberikan perintah kepada komputer tidak berlaku kebebasan berekspresi seperti laiknya dalam bahasa alamiah.
Pemrograman dalam pengertian luas meliputi seluruh kegiatan yang tercakup dalam pembuatan program, termasuk analisis kebutuhan (requirement’s analysis) dan keseluruhan tahapan dalam perencanaan (planning) , perancangan (design) dan pewujudannya (implementation).
Simulasi dibuat dengan menggunakan program Pascal, dengan terlebih dahulu harus dibuat suatu algoritmanya. Berikut algoritma program untuk menghitung nilai phi1 sebagai berikut:
1. Mulai
2. Ditetapkan i:=0
3. i:=i+1
4. Dibangkitkan 10000 titik
x ~ U(0,1) dan y ~ U(0,1)
5. Ditetapkan nilai phi:=4*m/n
6. Jika i < 1000 kembali ke langkah 3
7. Nilai phi sama dengan jumlahan dari tiap phi dibagi 1000
8. Ditulis nilai phi
9. Selesai
Hasil simulasi menggunakan program pascal :
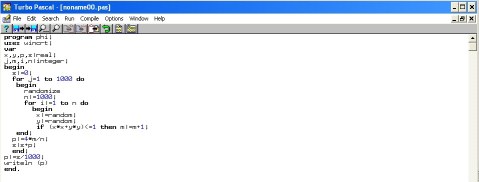
program phi1;
uses wincrt;
var x,y,p:real;
i,m,n:integer;
begin
randomize;
n:=10000;
m:=0;
for i:=1 to n do
begin
x:=random;
y:=random;
if(x*x+y*y)<=1 then m:=m+1; end; p:=4*m/n; writeln(p); end.
Selanjutnya akan dibuat program kedua dengan menambah variabel s yaitu sebagai banyaknya sampel yang diambil diulang sampai 1000 kali sebagai berikut : program phi2; uses wincrt; var x,y,p,s:real; j,i,m,n:integer; begin s:=0; begin randomize; n:=10000; m:=0; for i:=1 to n do begin x:=random; y:=random; if(x*x+y*y)<=1 then m:=m+1; end; p:=4*m/n; s:=s+p; end; p:=s/1000; writeln(p); end.
bila diterapkan pada program dhelpi adalah sebagai berikut:
Program
Var x,y,p,s:real;
J,i,m,n:integer;
Begin
S:=0;
For j:=1 to 1000 do
Begin
Randomize;
N:-1000; m:=0;
For i:=1 to n do
Begin
X:=random;
Y:=random;
If (x*x+y*y) <=1 then m:=m+1;
End;
P:=4*m/n; s:=s+p;
P:=s/1000;
Writeln (p);
End.
http://dzulcyber.blogspot.com/2008/08/download-pascal-tutorial.html
Langganan:
Postingan (Atom)
